BOJ 2579 - 계단 오르기 | Rust 풀이

1. 문제 분석

백준 2579 - 계단 오르기

위 문제의 핵심 조건과 목표을 정리하면 다음과 같이 요약할 수 있습니다.

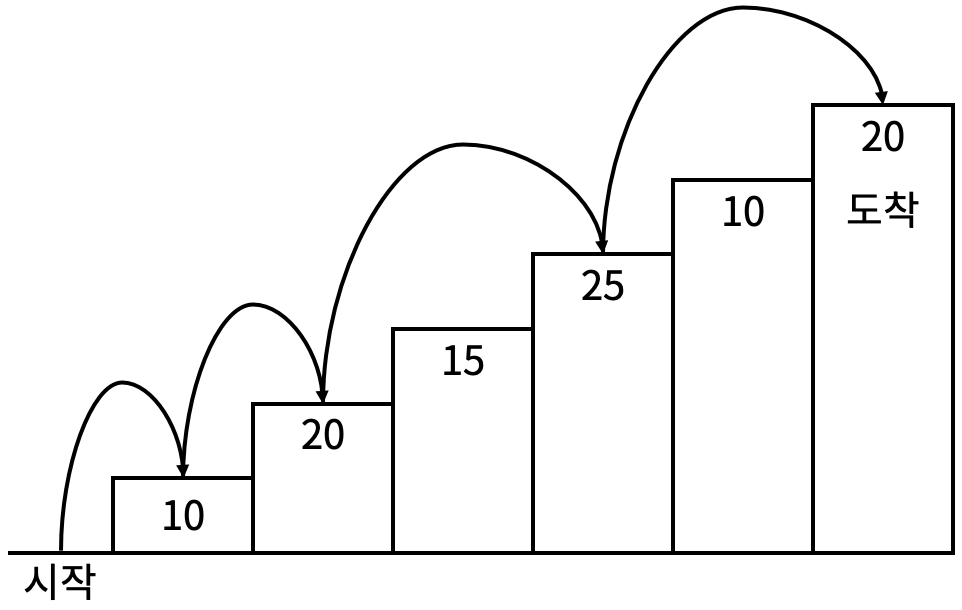
1. 계단은 한 번에 한 계단씩 또는 두 계단씩 오를 수 있다. 즉, 한 계단을 밟으면서 이어서 다음 계단이나, 다음 다음 계단으로 오를 수 있다.
2. 연속된 세 개의 계단을 모두 밟아서는 안 된다. 단, 시작점은 계단에 포함되지 않는다.
3. 마지막 계단은 반드시 밟아야 한다.

최종적으로 마지막 계단에 도달했을 때의 점수 합의 최댓값을 구하는 것이 목표입니다.

2. 접근 방법

이 문제는 동적 계획법(Dynamic Programming, DP)을 사용하여 해결할 수 있습니다.

왜 DP를 선택했는가?

• 이 문제는 이전 단계까지의 최적해(작은 문제)를 이용하여 현재의 최적해(큰 문제)를 구할 수 있는 구조이므로, 계산 결과를 저장하고 재활용하는 DP가 가장 적합합니다.

2.1. 핵심 아이디어

“도착지($N$)을 기준으로 역추적하기”

위 문제를 곰곰히 생각해보면, 마지막 계단($N$)에 도달하기 위해서는 두 가지 방법이 있음을 알 수 있습니다.

1. 전전 계단($N-2$)에서 점프: 2칸을 뛰었으므로 연속 3계단 규칙에 걸리지 않음.
2. 직전 계단($N-1$)에서 걷기: 규칙 위반(3연속)을 막기 위해, 그 전에는 반드시 점프($N-3 \rightarrow N-1$)해서 왔어야 함.

이를 바탕으로 다음과 같은 점화식을 도출할 수 있습니다.

\[dp[i] = \max \begin{cases} dp[i-2] + score[i] & \text{(2칸 점프)} \\ dp[i-3] + score[i-1] + score[i] & \text{(직전 점프 후 1칸)} \end{cases}\]

2.2. DP 테이블 정의 및 초기값

이제 위에서 도출한 점화식을 바탕으로 DP 테이블을 정의해보겠습니다.

• 배열 정의
  • stairs[i-1]: i번째 계단의 점수
  • dp[i-1]: i번째 계단에 도달했을 때의 최대 점수
• 초기값 설정
  • dp[0] = stairs[0]
  • dp[1] = stairs[0] + stairs[1]
  • dp[2] = max(stairs[0] + stairs[2], stairs[1] + stairs[2])

3. 코드 구현 (Rust)

자세한 코드는 여기에서 확인할 수 있습니다.

use std::cmp::max;

fn solution(stdin: &str) {
    let mut lines = stdin.lines();

    // 계단 개수와 점수 입력
    let n: usize = lines.next().unwrap().parse().unwrap();
    let stairs: Vec<u32> = lines
        .map(|line| line.parse().unwrap())
        .collect();

    // 예외 처리: 계단이 1개 또는 2개인 경우
    if n == 1 {
        println!("{}", stairs[0]);
        return;
    } else if n == 2 {
        println!("{}", stairs[0] + stairs[1]);
        return;
    }

    // idx 번째 계단에 도달했을 때의 최대 점수
    let mut dp = vec![0; n];
    dp[0] = stairs[0];             // 계단이 1개일 때, 첫 번째 계단은 무조건 밟음
    dp[1] = stairs[0] + stairs[1]; // 계단이 2개일 때, 두 계단 모두 밟음

    // 계단이 3개일 때, 3번째 계단은 1번째 or 2번째 계단에서 올 수 있음
    dp[2] = max(stairs[0] + stairs[2], stairs[1] + stairs[2]);

    // 점화식에 따라 dp 배열 채우기
    for i in 3..n {
        dp[i] = max(
            dp[i-2] + stairs[i],              // 2칸 점프
            dp[i-3] + stairs[i-1] + stairs[i] // 직전에 2칸 점프 후 1칸 점프
        )
    }

    // 마지막 계단에 도달했을 때의 최대 점수 출력
    println!("{}", dp[n - 1]);
}

4. 복잡도 분석

• 시간 복잡도: $O(N)$
  • 각 계단에 대해 한 번씩만 계산하므로, 선형 시간이 소요됩니다.
• 공간 복잡도: $O(N)$
  • DP 테이블을 저장하기 위해 $N$ 크기의 배열이 필요합니다.
  • (실제로는 직전 3개의 값만 있어도 계산이 가능하므로, 변수 스와핑(swap)을 통해 공간 복잡도를 $O(1)$로 줄일 수 있습니다.)